Visualisation d’une fonction de 2 variables#
Nous allons voir comment visualiser une fonction de deux variables f(x, y).
Dans cette page, nous présentons deux styles de programmation :
le style « pyplot » qui utilise directement des fonctions du module
pyplot;le style « Oriénté Objet (OO) » qui est recommandé dans la documentation de Matplotlib.
Pour plus d’informations sur la différence entre les deux syles, vous pouvez consulter la page Tracé de courbes.
Utilisation de meshgrid()#
Pour visualiser une fonction z = f(x, y) :
Il faut d’abord générer des tableaux X et Y (noms arbitraires) qui contiennent les valeurs des abscisses et ordonnées pour chacun des points grâce à la fonction
meshgrid().Ensuite il faut calculer la valeur de z pour chacun de ces points.
meshgrid() permet de générer un maillage.
>>> import numpy as np
>>> x = np.array([3, 4, 7])
>>> y = np.array([-1, 0])
>>> X, Y = np.meshgrid(x, y)
>>> X
array([[3, 4, 7],
[3, 4, 7]])
>>> Y
array([[-1, -1, -1],
[ 0, 0, 0]])
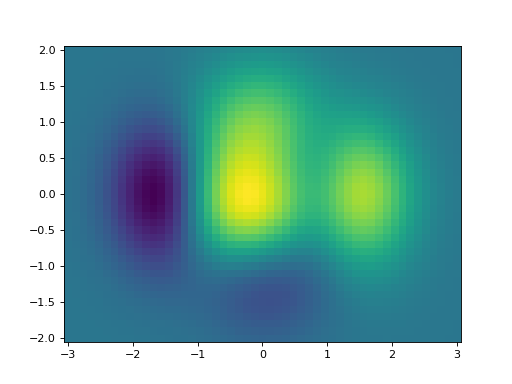
Utilisation de pcolormesh()#
pcolormesh() permet une visualisation grâce à des couleurs.
Style « pyplot »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
plt.pcolormesh(X, Y, Z)
plt.show()
Style « Orienté Objet »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
fig, ax = plt.subplots()
ax.pcolormesh(X, Y, Z)
plt.show()
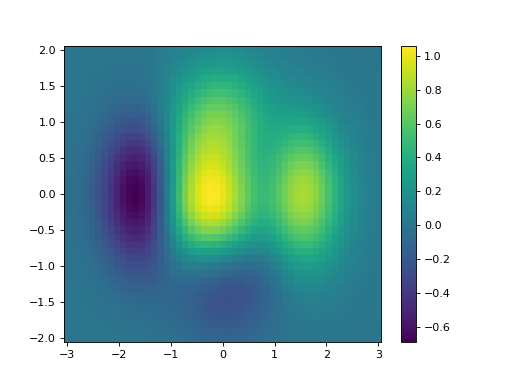
Affichage d’une échelle des couleurs - colorbar()#
Style « pyplot »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
plt.pcolormesh(X, Y, Z)
plt.colorbar()
plt.show()
Style « Orienté Objet »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
fig, ax = plt.subplots()
pc = ax.pcolormesh(X, Y, Z)
fig.colorbar(pc)
plt.show()
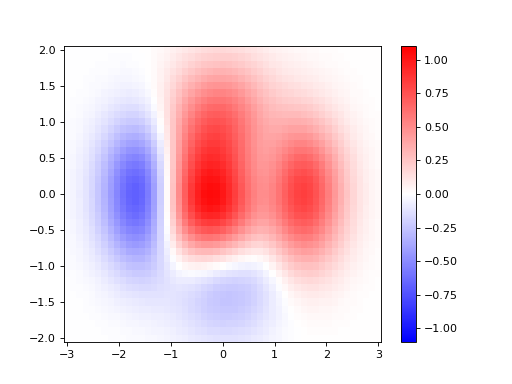
Changement de l’échelle des couleurs#
Il est possible de changer le domaine des couleurs en précisant les valeurs vmin et vmax. On peut également modifier l’échelle des couleurs (colormap) avec le paramètre cmap.
Voici un exemple avec l’échelle bwr pour blue-white-red.
Style « pyplot »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
plt.pcolormesh(X, Y, Z, vmin=-1.1, vmax = 1.1, cmap=plt.cm.bwr)
plt.colorbar()
plt.show()
Style « Orienté Objet »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
fig, ax = plt.subplots()
pc = ax.pcolormesh(X, Y, Z, vmin=-1.1, vmax = 1.1, cmap=plt.cm.bwr)
fig.colorbar(pc)
plt.show()
Note
Vous pouvez consulter les différentes échelles de couleurs avec le lien suivant : https://matplotlib.org/stable/gallery/color/colormap_reference.html
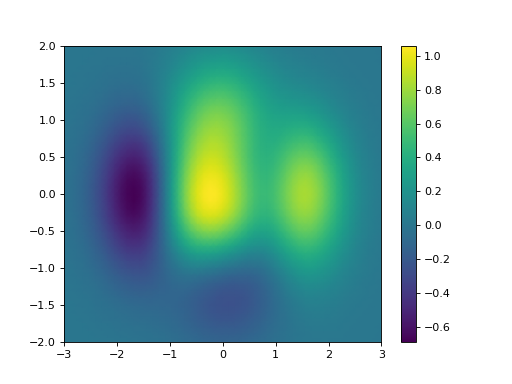
Mise en place d’un effet de fondu sur les couleurs#
On peut mettre en place un effet de fondu sur les couleurs pour éviter l’aspect quadrillage grâce à l’argument shading="gouraud".
Style « pyplot »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
plt.pcolormesh(X, Y, Z, shading="gouraud")
plt.colorbar()
plt.show()
Style « Orienté Objet »
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 51)
y = np.linspace(-2, 2, 41)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
fig, ax = plt.subplots()
pc = ax.pcolormesh(X, Y, Z, shading="gouraud")
fig.colorbar(pc)
plt.show()
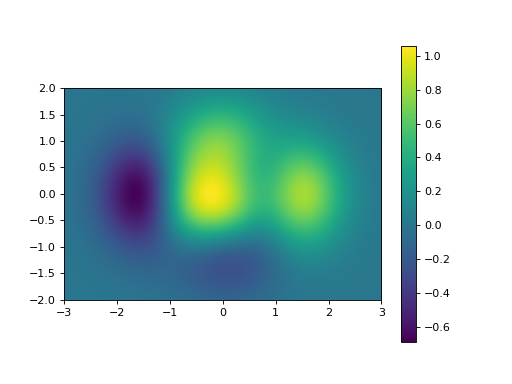
Utilisation de imshow()#
Style « pyplot »
import numpy as np
import matplotlib.pyplot as plt
xmin = -3
xmax = 3
nbx = 51
ymin = -2
ymax = 2
nby = 41
x = np.linspace(xmin, xmax, nbx)
y = np.linspace(ymin, ymax, nby)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
plt.imshow(Z, interpolation="bicubic",
origin="lower", extent=[xmin,xmax,ymin,ymax])
plt.colorbar()
plt.show()
Style « Orienté Objet »
import numpy as np
import matplotlib.pyplot as plt
xmin = -3
xmax = 3
nbx = 51
ymin = -2
ymax = 2
nby = 41
x = np.linspace(xmin, xmax, nbx)
y = np.linspace(ymin, ymax, nby)
X, Y = np.meshgrid(x, y)
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2) # calcul du tableau des valeurs de Z
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation="bicubic",
origin="lower", extent=[xmin,xmax,ymin,ymax])
fig.colorbar(im)
plt.show()
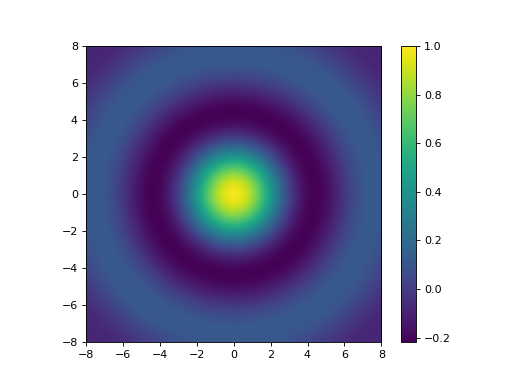
Exemple : visualisation de la fonction sinus cardinal#
Nous allons tracer la fonction sinus cardinal (plus précisément ici sin(r)/r). On va utiliser la constante prédéfinie finfo(float).eps pour lever l’indétermination de la division 0/0.
Note
finfo(float).eps est le plus petit flottant positif tel que 1.0 + eps != 1.0. eps = 2**(-52), ce qui donne approximativement 2.22e-16.
Style « pyplot »
import numpy as np
import matplotlib.pyplot as plt
epsilon = np.finfo(float).eps
print("epsilon =", epsilon)
xmin = -8
xmax = 8
nbx = 41
ymin = -8
ymax = 8
nby = 41
x = np.linspace(xmin, xmax, nbx)
y = np.linspace(ymin, ymax, nby)
X, Y = np.meshgrid(x, y)
R = np.sqrt(X**2 + Y**2) + epsilon
Z = np.sin(R) / R
plt.imshow(Z, interpolation="bicubic",
origin="lower", extent=[xmin,xmax,ymin,ymax])
plt.colorbar()
plt.show()
Style « Orienté Objet »
import numpy as np
import matplotlib.pyplot as plt
epsilon = np.finfo(float).eps
print("epsilon =", epsilon)
xmin = -8
xmax = 8
nbx = 41
ymin = -8
ymax = 8
nby = 41
x = np.linspace(xmin, xmax, nbx)
y = np.linspace(ymin, ymax, nby)
X, Y = np.meshgrid(x, y)
R = np.sqrt(X**2 + Y**2) + epsilon
Z = np.sin(R) / R
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation="bicubic",
origin="lower", extent=[xmin,xmax,ymin,ymax])
fig.colorbar(im)
plt.show()
Voir aussi
