Intégration par la méthode de Simpson#
Il existe de nombreuses méthodes pour réaliser une intégration numérique. Nous allons considérer la méthode de Simpson. Ceux qui souhaiteraient aller plus loin peuvent consulter par exemple Pratique de la simulation numérique de Bijan Mohammadi et Jacques Hervé Saïac, Dunod (2003).
La méthode de Simpson permet le calcul approché d’une intégrale avec la formule suivante :
Dans cette formule, on peut se demander d’où viennent les coefficients \(\frac{1}{6}\) et \(\frac{2}{3}\) (qui apparaît sous la forme de \(\frac{4}{6}\)).
C’est ce que nous allons voir de façon détaillée maintenant.
Pour obtenir la formule de Simpson, on va réaliser une interpolation avec un polynôme de degré 2. Un polynôme étant une fonction très facile à intégrer, on approche l’intégrale de la fonction \(f\) sur l’intervalle \(\left[ a,b \right]\), par l’intégrale du polynôme sur ce même intervalle.
Interpolation par un polynôme de degré 2#
Une interpolation qui passe par 3 points peut être réalisée grâce à un polynôme de degré 2. Dans le cas de la méthode de Simpson, le polynôme va prendre les mêmes valeurs que \(f\) aux points d’abscisses \(a\), \(b\) et \(m = (a + b)/2\). La technique utilisée pour déterminer le polynôme est basée sur les polynômes de Lagrange, on parle d”interpolation lagrangienne.
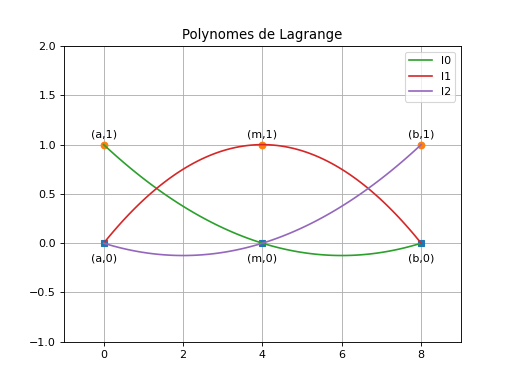
Les polynômes de Lagrange de degré 2 ont pour caractéristique de prendre la valeur 1 pour une seule des 3 abscisses et la valeur 0 pour les 2 autres. On définit ainsi 3 polynômes :
\(l_0(x) = \frac{(x-m)(x-b)}{(a-m)(a-b)}\) qui prend pour valeur 1 en \(x=a\) et 0 en \(m\) et \(b\).
\(l_1(x) = \frac{(x-a)(x-b)}{(m-a)(m-b)}\) qui prend pour valeur 1 en \(x=m\) et 0 en \(a\) et \(b\).
\(l_2(x) = \frac{(x-a)(x-m)}{(b-a)(b-m)}\) qui prend pour valeur 1 en \(x=b\) et 0 en \(a\) et \(m\).
Visualisation des polynômes de Lagrange
import numpy as np
import matplotlib.pyplot as plt
a = 0
b = 8
m = (a+b)/2
x = np.linspace(a, b, 101)
l0 = (x-m)/(a-m)*(x-b)/(a-b)
l1 = (x-a)/(m-a)*(x-b)/(m-b)
l2 = (x-a)/(b-a)*(x-m)/(b-m)
plt.plot([a,m,b],np.zeros(3),"s") # position des valeurs 0
plt.plot([a,m,b],np.ones(3), "o") # position des valeurs 1
plt.plot(x,l0, label="l0")
plt.plot(x,l1, label="l1")
plt.plot(x,l2, label="l2")
plt.title("Polynomes de Lagrange")
plt.xlim(-1,9)
plt.ylim(-1,2)
plt.text(a,-0.1,"(a,0)",ha="center",va="top")
plt.text(m,-0.1,"(m,0)",ha="center",va="top")
plt.text(b,-0.1,"(b,0)",ha="center",va="top")
plt.text(a,1.05,"(a,1)",ha="center",va="bottom")
plt.text(m,1.05,"(m,1)",ha="center",va="bottom")
plt.text(b,1.05,"(b,1)",ha="center",va="bottom")
plt.legend()
plt.grid()
plt.show()
Le polynôme \(P\) de degré 2 qui prend les mêmes valeurs que \(f\) aux points d’abscisses \(a\), \(b\) et \(m\) peut être écrit sous la forme suivante :
Exemple d’interpolation de Lagrange avec un polynôme de degré 2
import numpy as np
import matplotlib.pyplot as plt
a = 0
b = 8
m = (a+b)/2
# valeurs de la fonction en a, m, et b
ya = 4
ym = 8
yb = -6
x = np.linspace(a, b, 101)
l0 = (x-m)/(a-m)*(x-b)/(a-b)
l1 = (x-a)/(m-a)*(x-b)/(m-b)
l2 = (x-a)/(b-a)*(x-m)/(b-m)
P = ya*l0 + ym*l1 + yb*l2
plt.plot([a,m,b],np.zeros(3),"s") # position des valeurs 0
plt.plot([a,m,b],[ya,ym,yb], "o") # position des valeurs de f
plt.plot(x,P)
plt.title("Interpolation de Lagrange")
plt.xlim(-1,9)
plt.ylim(-8,10)
plt.text(a,-0.5,"(a,0)",ha="center",va="top")
plt.text(m,-0.5,"(m,0)",ha="center",va="top")
plt.text(b,-0.5,"(b,0)",ha="center",va="top")
plt.text(a,ya+0.05,"(a,f(a))",ha="right",va="bottom")
plt.text(m,ym+0.2,"(m,f(m))",ha="left",va="bottom")
plt.text(b,yb-0.4,"(b,f(b))",ha="left",va="top")
plt.grid()
plt.show()
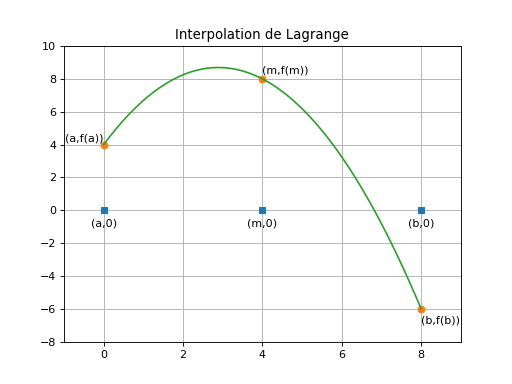
La courbe rouge représente le polynôme d’interpolation \(P\).
Intégration des polynômes de Lagrange#
Un polynôme étant une fonction très facile à intégrer, on approche l’intégrale de la fonction \(f\) sur l’intervalle \(\left[ a,b \right]\), par l’intégrale de \(P\) sur ce même intervalle. Pour cela, nous allons calculer les intégrales des 3 polynômes de Lagrange.
Considérons tout d’abord le calcul de l’intégrale du polynôme de Lagrange \(l_2\).
Le calcul de cette intégrale n’est pas immédiat et nous allons détailler une façon de réaliser ce calcul.
On va poser \(k=\frac{b-a}{2}\), ainsi \(k=m-a=b-m\).
Nous faisons ensuite le changement de variable suivant : \(u=\frac{x-m}{k}\), ainsi \(du=\frac{dx}{k}\).
Pour \(x=a\), on a \(u=-1\). De même, pour \(x=b\), on a \(u=1\).
\(\frac{x-a}{b-a}=\frac{(x-m)+(m-a)}{a-b}=\frac{x-m}{b-a}+\frac{m-a}{b-a}=\frac{x-m}{2k}+\frac{k}{2k}=\frac{u}{2}+\frac{1}{2}=\frac{u+1}{2}\)
\(\frac{x-m}{b-m}=u\)
\(\int_{a}^{b}{{{l}_{2}}}(x)dx=k\int_{-1}^{1}{\frac{(u+1)}{2}u}du=\frac{k}{2}\int_{-1}^{1}{({{u}^{2}}+u)du}=\frac{k}{2}2\int_{0}^{1}{{{u}^{2}}du}\)
car on intègre sur un intervalle symétrique et \(u^2\) est une fonction paire et \(u\) impaire.
Ainsi, \(\int_{a}^{b}{{{l}_{2}}}(x)dx=k\left[ \frac{{{u}^{3}}}{3} \right]_{0}^{1}=\frac{k}{3}\)
Au final :
On comprend donc ici l’origine du facteur \(\frac{1}{6}\).
On peut obtenir de même :
Pour \({{l}_{1}}\), on a :
\(\int_{a}^{b}{{{l}_{1}}}(x)dx=\int_{a}^{b}{\frac{(x-a)(x-b)}{(m-a)(m-b)}}dx\)
\(\frac{x-a}{m-a}=\frac{(x-m)+(m-a)}{m-a}=u+1\)
\(\frac{x-b}{m-b}=\frac{(x-m)+(m-b)}{m-b}=-u+1\)
\(\int_{a}^{b}{{{l}_{1}}}(x)dx=k\int_{-1}^{1}{(u+1)(-u+1)}du=k\int_{-1}^{1}{(1-{{u}^{2}})du}=2k\int_{0}^{1}{(1-{{u}^{2}})du}\)
car on intègre sur un intervalle symétrique et \(1\) et \({{u}^{2}}\) sont des fonctions paires.
Ainsi, \(\int_{a}^{b}{{{l}_{1}}}(x)dx=2k\left[ u-\frac{{{u}^{3}}}{3} \right]_{0}^{1}=2k\frac{2}{3}\)
Au final :
On a donc ici l’origine du facteur \(\frac{2}{3}\).
Formule de Simpson#
En utilisant les résultats des 3 intégrales, on obtient ainsi la simple formule :
C’est la formule de Simpson.
Formule de Simpson composite#
Par ailleurs, plus l’intervalle est petit, meilleure est l’approximation de la valeur de l’intégrale. Par conséquent, pour obtenir un résultat correct, on subdivise l’intervalle \(\left[ a,b \right]\) en un nombre pair de sous-intervalles et on additionne la valeur obtenue sur chaque sous-intervalle. On a ainsi :
\(n\) est le nombre de sous-intervalles de \(\left[ a,b \right]\) avec \(n\) pair ;
\(h=(b-a)/n\) est la longueur de ces sous-intervalles ;
\(x_i=a+ih\) pour \(i=0, 1, \dots, n-1, n\).
Exemple
Nous allons illustrer le cas où \(n = 4\). On a 5 points : \(x_0,x_1, x_2,x_3,x_4\). On applique deux fois la formule de Simpson : une fois pour le sous-intervalle \(\left[ {{x}_{0}},{{x}_{2}} \right]\) et une fois pour le sous-intervalle \(\left[ {{x}_{2}},{{x}_{4}} \right]\).
Or \({{x}_{2}}-{{x}_{0}}={{x}_{4}}-{{x}_{2}}=2h\), donc au final :
Ceci est bien conforme à la formule de Simpson composite énoncée ci-dessus.
Exercice
Faire un programme d’intégration numérique qui utilise la formule de Simpson composite.
