Dérivée d’une fonction en Python#
Fiche pratique : comment calculer numériquement la dérivée d’une fonction ?
Cette page présente le calcul numérique de la dérivée d’une fonction dont on connait les valeurs \(f(x)\) pour des abscisses \(x_i\).
Une dérivation numérique peut se faire simplement en calculant la pente de la courbe.
Nous allons considérer que nous disposons au préalable des valeurs de la fonction en \(nbx\) points de coordonnées \((x_i, y_i)\) où \(y_i = f(x_i)\). Le nom de variable \(nbx\) est choisi pour signifier nombre de x.
Une approximation numérique de la dérivée est obtenue en calculant la pente entre deux points de coordonnées \((x_i, y_i)\) et \((x_{i+1}, y_{i+1})\).
La pente correspond au coefficient directeur de la droite qui passe par ces deux points.
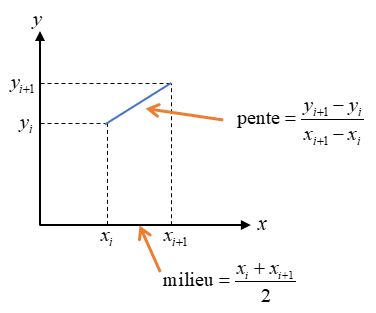
Comme la pente est calculée entre deux abscisses \(x_i\) et \(x_{i+1}\), on associera cette dérivée à l’abscisse située au milieu.
On stocke les valeurs des nouvelles abscisses dans un tableau \(\text{xnew}\). Ainsi, \(\text{xnew}_i = (x_i + x_{i+1})/2\).
Il est important de noter qu’il y aura seulement \(nbx-1\) valeurs pour \(\text{xnew}\).
Nous donnons ici un premier programme qui utilise une boucle pour calculer les valeurs de la dérivée qui seront stockées dans un tableau \(\text{yp}\) avec :
Remarque : le tableau est nommé \(\text{yp}\) pour \(\text{y}\) prime, car le prime (symbole \”) est associé à la dérivée.
Exemple de programme#
Calcul de la dérivée de la fonction cosinus
import numpy as np
import matplotlib.pyplot as plt
nbx = 101
x = np.linspace(0, 10, nbx)
y = np.cos(x)
# préparation des tableaux qui vont recevoir les valeurs
xnew = np.zeros(nbx-1)
yp = np.zeros(nbx-1)
# calcul des abscisses et des valeurs de la dérivée
for i in range(nbx-1):
xnew[i] = (x[i] + x[i+1]) / 2
yp[i] = (y[i+1] - y[i]) / (x[i+1] - x[i])
plt.plot(x, y, label="f(x)")
plt.plot(xnew, yp, label="f'(x)")
plt.legend()
plt.show()
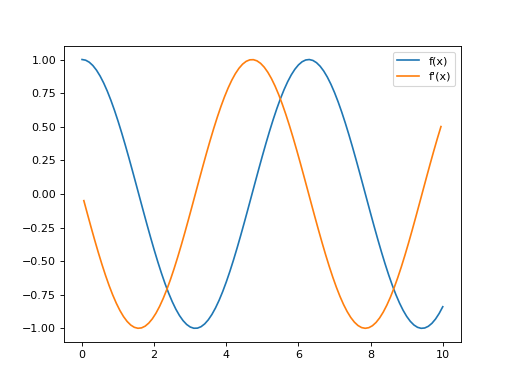
La technique que nous venons d’utiliser pour calculer la dérivée correspond à une méthode de différence finie centrée car elle associe la valeur de la dérivée à une abscisse située au centre entre \(x_i\) et \(x_{i+1}\).
L’avantage de cette méthode est qu’elle respecte une certaine symétrie entre les abscisses qui permettent le calcul et la position située au centre à laquelle on associe la valeur de la dérivée.
L’inconvénient est qu’elle nécessite de créer un tableau supplémentaire pour stocker les nouvelles abscisses.
Pour éviter cela, il est possible d’associer la valeur de la dérivée à une des deux abscisses déjà connues \(x_i\) ou \(x_{i+1}\).
Si on utilise \(x_i\), on obtient le programme suivant :
import numpy as np
import matplotlib.pyplot as plt
nbx = 101
x = np.linspace(0, 10, nbx)
y = np.cos(x)
# préparation du tableau qui va recevoir les valeurs
yp = np.zeros(nbx-1)
# calcul des valeurs de la dérivée
for i in range(nbx-1):
yp[i] = (y[i+1] - y[i]) / (x[i+1] - x[i])
plt.plot(x, y, label="f(x)")
plt.plot(x[0:nbx-1], yp, label="f'(x)")
plt.legend()
plt.show()
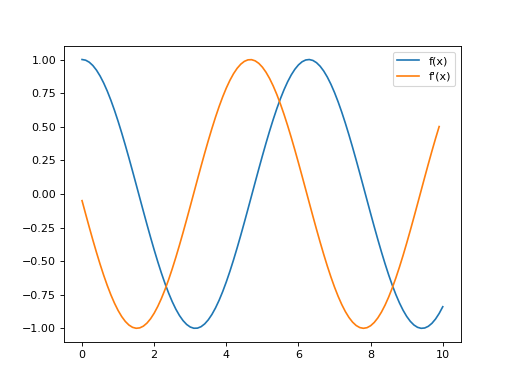
On constate que lorsque le pas entre les valeurs de \(x\) est petit, on ne voit pas de différence avec la méthode centrée précédente.
A noter : pour la dérivée, il n’y a que \(nbx-1\) abscisses qui sont utilisées.
Exemples avec vectorisation du calcul#
Pour faciliter la compréhension et permettre à ceux qui ne connaissent pas la technique du slicing offerte par NumPy, nous avons donné des programmes qui utilisaient une boucle pour le calcul de la dérivée. Toutefois, , le slicing permet de vectoriser le calcul, ce qui le rend plus rapide et évite de recourir une boucle.
Voici de nouvelles versions des programmes précédents avec la technique du slicing.
Exemple avec la méthode centrée
import numpy as np
import matplotlib.pyplot as plt
nbx = 101
x = np.linspace(0, 10, nbx)
y = np.cos(x)
# calcul des abscisses et des valeurs de la dérivée
xnew = (x[:-1] + x[1:]) / 2
yp = (y[1:] - y[:-1]) / (x[1:] - x[:-1])
plt.plot(x, y, label="f(x)")
plt.plot(xnew, yp, label="f'(x)")
plt.legend()
plt.show()
Exemple sans tableau xnew
import numpy as np
import matplotlib.pyplot as plt
nbx = 101
x = np.linspace(0, 10, nbx)
y = np.cos(x)
# calcul des valeurs de la dérivée
yp = (y[1:] - y[:-1]) / (x[1:] - x[:-1])
plt.plot(x, y, label="f(x)")
plt.plot(x[:-1], yp, label="f'(x)")
plt.legend()
plt.show()
Exemple dans le cas particulier d’un pas constant
Dans le cas particulier où l’espacement entre les valeurs de \(x\) est constant, il est possible de simplifier le calcul de la pente en divisant par le pas \(h\). On a alors :
import numpy as np
import matplotlib.pyplot as plt
nbx = 101
x = np.linspace(0, 10, nbx)
y = np.cos(x)
h = x[1]-x[0] # calcul du pas
# calcul des valeurs de la dérivée
yp = (y[1:] - y[:-1]) / h
plt.plot(x, y, label="f(x)")
plt.plot(x[:-1], yp, label="f'(x)")
plt.legend()
plt.show()
