Approximation de la transformée de Fourier spatiale grâce à la FFT#
Présentation#
Pour une introduction à la FFT en Python, vous pouvez consulter la page Transformation de Fourier, FFT et DFT.
Nous allons considérer l’expression suivante pour la transformée de Fourier :
\(g(k) = \frac{1}{\sqrt{2 \pi}}\int\limits_{-\infty}^{+\infty} f(x) e^{- i k x}dx\)
Lorsqu’on désire calculer la transformée de Fourier de la fonction \(f(x)\) à l’aide d’un ordinateur, ce dernier ne travaille que sur des valeurs discrètes, on est amené à :
discrétiser la fonction spatiale,
tronquer la fonction spatiale,
discrétiser la fonction des fréquences spatiales.
En approchant l’intégrale par une somme d’aires de rectangles de largeur \(\Delta x\) et en limitant la domaine d’intégration à un intervalle de longueur \(n \Delta x\), c’est-à-dire en faisant une somme pour \(n\) valeurs \(x_m = m \Delta x\) avec \(m\) allant de \(0\) à \(n-1\), on obtient :
\(g(k) \approx \frac{\Delta x}{\sqrt{2 \pi}}\sum\limits_{m=0}^{n-1}{ f(x_m) e^{-i k x_m}}\)
Or, si on choisit des fréquences spatiales discrètes telles que \(k_j = j \frac{2\pi}{n \Delta x}\), on a \(k_j x_m = j \frac{2\pi}{n \Delta x} \, m \Delta x = 2\pi\frac{j m}{n}\):
\(g(k_j) \approx \frac{\Delta x}{\sqrt{2 \pi}} \sum\limits_{m=0}^{n-1}{ f(x_m) e^{-i k_j x_m} } \approx \frac{\Delta x}{\sqrt{2 \pi}} \sum\limits_{m=0}^{n-1}{ f(x_m) e^{-2\pi i \frac{j m}{n}}}\approx \frac{\Delta x}{\sqrt{2 \pi}} \,\text{fft}(f)\)
Exemple dans le cas d’une gaussienne#
import numpy as np
import matplotlib.pyplot as plt
alpha = 20
nc = 40
dx = 0.1
xmax = (nc-1) * dx
xmin = -nc * dx
# definition d'un signal gaussien
x = np.linspace(xmin, xmax, 2*nc)
f = np.exp(-alpha/2 * x**2)
plt.subplot(411)
plt.plot(x,f)
# on effectue un ifftshift pour positionner le temps zero comme premier element
plt.subplot(412)
a = np.fft.ifftshift(f)
plt.plot(a)
A = np.fft.fft(a)
# on effectue un fftshift pour positionner la frequence zero au centre
g = dx/np.sqrt(2*np.pi)*np.fft.fftshift(A)
# calcul des frequences avec fftfreq
n = x.size
freq = 2*np.pi * np.fft.fftfreq(n, d=dx)
k = np.fft.fftshift(freq)
# comparaison avec la solution exacte
plt.subplot(413)
plt.plot(k, np.real(g), label="fft")
plt.plot(k, 1/np.sqrt(alpha) * np.exp( -k**2 / (2*alpha)), label="exact")
plt.legend()
plt.subplot(414)
plt.plot(k, np.imag(g))
plt.show()
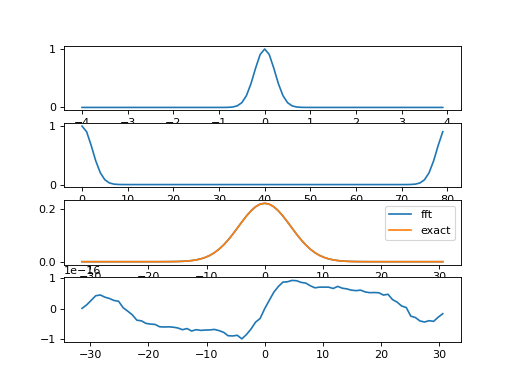
Pour vérifier notre calcul, nous avons utilisé une transformée de Fourier connue. En effet, pour la définition utilisée, la transformée de Fourier d’une gaussienne \(e^{-\alpha \frac{x^2}{2}}\) est donnée par :
\(\frac{1}{\sqrt{\alpha}}e^{-\frac{k^2}{2\alpha}}\)
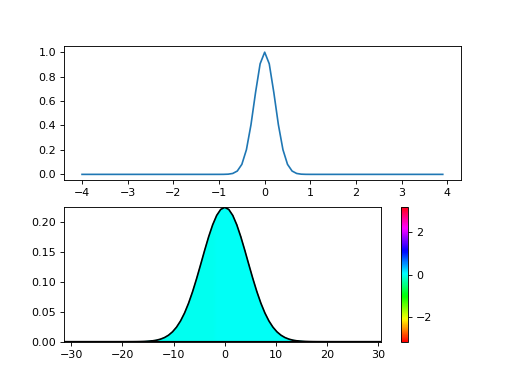
Exemple avec visualisation en couleur de la transformée de Fourier#
import numpy as np
import matplotlib.pyplot as plt
alpha = 20
nc = 40
dx = 0.1
xmax = (nc-1) * dx
xmin = -nc * dx
# definition d'un signal gaussien
x = np.linspace(xmin, xmax, 2*nc)
f = np.exp(-alpha/2 * x**2)
plt.subplot(211)
plt.plot(x,f)
# on effectue un ifftshift pour positionner le temps zero comme premier element
a = np.fft.ifftshift(f)
A = np.fft.fft(a)
# on effectue un fftshift pour positionner la frequence zero au centre
g = dx/np.sqrt(2*np.pi)*np.fft.fftshift(A)
# calcul des frequences avec fftfreq
n = x.size
freq = 2*np.pi * np.fft.fftfreq(n, d=dx)
k = np.fft.fftshift(freq)
# visualisation de X - Attention au changement de variable
# on ajoute a droite la valeur de gauche pour la periodicite
plt.subplot(212)
x = np.append(k, k[0]) # calcul d'une valeur supplementaire
z = np.append(g, g[0])
X = np.array([x,x])
y0 = np.zeros(len(x))
y = np.abs(z)
Y = np.array([y0,y])
Z = np.array([z,z])
C = np.angle(Z)
plt.plot(x,y,'k')
plt.pcolormesh(X, Y, C, shading="gouraud", cmap=plt.cm.hsv, vmin=-np.pi, vmax=np.pi)
plt.colorbar()
plt.show()
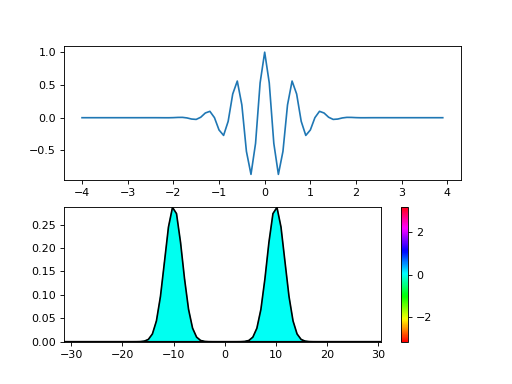
Exemple pour le produit d’un cosinus par une gaussienne#
import numpy as np
import matplotlib.pyplot as plt
alpha = 3
k1 = 10
nc = 40
dx = 0.1
xmax = (nc-1) * dx
xmin = -nc * dx
# definition d'un signal gaussien
x = np.linspace(xmin, xmax, 2*nc)
f = np.cos(k1*x)*np.exp(-alpha/2 * x**2)
plt.subplot(211)
plt.plot(x,f)
# on effectue un ifftshift pour positionner le temps zero comme premier element
a = np.fft.ifftshift(f)
A = np.fft.fft(a)
# on effectue un fftshift pour positionner la frequence zero au centre
g = dx/np.sqrt(2*np.pi)*np.fft.fftshift(A)
# calcul des frequences avec fftfreq
n = x.size
freq = 2*np.pi * np.fft.fftfreq(n, d=dx)
k = np.fft.fftshift(freq)
# visualisation de X - Attention au changement de variable
# on ajoute a droite la valeur de gauche pour la periodicite
plt.subplot(212)
x = np.append(k, k[0]) # calcul d'une valeur supplementaire
z = np.append(g, g[0])
X = np.array([x,x])
y0 = np.zeros(len(x))
y = np.abs(z)
Y = np.array([y0,y])
Z = np.array([z,z])
C = np.angle(Z)
plt.plot(x,y,'k')
plt.pcolormesh(X, Y, C, shading="gouraud", cmap=plt.cm.hsv, vmin=-np.pi, vmax=np.pi)
plt.colorbar()
plt.show()