Tableaux et calcul matriciel avec PyLab#
Nous allons voir comment créer des tableaux avec la fonction array() de la bibliothèque NumPy. Ces tableaux pourront être utilisés comme des vecteurs ou des matrices grâce à des fonctions de NumPy (dot(), det(), inv(), eig(), etc.) qui permettent de réaliser des calculs matriciels utilisés en algèbre linéaire.
Nous allons travailler en interactif.
Dans cette page, nous allons utiliser la syntaxe « PyLab » qui est proche de celle de Matlab. Pour cela, il suffit de faire :
from pylab import *
Il est alors possible d’accéder directement aux fonctions de NumPy et Matplotlib.
Si vous ne souhaitez pas utiliser la syntaxe « PyLab » et si vous préférez faire une importation du module numpy, vous pouvez consulter la page Tableaux et calcul matriciel avec NumPy.
Tableaux - array()#
Pour créer des tableaux, nous allons utiliser array().
Tableaux monodimensionnels (1D)#
Pour créer un tableau 1D, il suffit de passer une liste de nombres en argument de array(). Un liste est constituée de nombres séparés par des virgules et entourés de crochets ([ et ]).
>>> a = array([4,7,9])
>>> a
array([4, 7, 9])
>>> print(a)
[4 7 9]
Pour connaître le type du résultat de array(), on peut utiliser la fonction type().
>>> type(a)
<type 'numpy.ndarray'>
On constate que ce type est issu du package numpy. Ce type est différent de celui d’une liste.
>>> type([4, 7, 9])
<type 'list'>
Tableaux bidimensionnels (2D)#
Pour créer un tableau 2D, il faut transmettre à array() une liste de listes grâce à des crochets imbriqués.
>>> a = array([[1, 2, 3], [4, 5, 6]])
>>> a
array([[1, 2, 3],
[4, 5, 6]])
La fonction size()#
La fonction size() renvoie le nombre d’éléments du tableau.
>>> a = array([2,5,6,8])
>>> size(a)
4
>>> b = array([[1, 2, 3],
[4, 5, 6]])
>>> size(b)
6
La fonction shape()#
La fonction shape() (forme, en anglais) renvoie la taille du tableau.
>>> a = array([2,5,6,8])
>>> shape(a)
(4,)
>>> b = array([[1, 2, 3],
[4, 5, 6]])
>>> shape(b)
(2, 3)
On distingue bien ici que a et b correspondent à des tableaux 1D et 2D, respectivement.
Produit terme à terme#
Il est possible de réaliser un produit terme à terme grâce à l’opérateur *. Il faut dans ce cas que les deux tableaux aient la même taille.
>>> a = array([[1, 2, 3],
[4, 5, 6]])
>>> b = array([[2, 1, 3],
[3, 2, 1]])
>>> a*b
array([[ 2, 2, 9],
[12, 10, 6]])
Produit matriciel - dot()#
Un tableau peut jouer le rôle d’une matrice si on lui applique une opération de calcul matriciel. Par exemple, la fonction dot() permet de réaliser le produit matriciel.
>>> a = array([[1, 2, 3],
[4, 5, 6]])
>>> b = array([[4],
[2],
[1]])
>>> dot(a,b)
array([[11],
[32]])
Le produit d’une matrice de taille n x m par une matrice m x p donne une matrice n x p.
A partir de la version 3.5 de Python, il est également possible d’effectuer le produit matriciel en utilisant @.
>>> a @ b
array([[11],
[32]])
Transposé#
>>> a.T
array([[1, 4],
[2, 5],
[3, 6]])
Complexe conjugué - conj()#
>>> u = array([[ 2j, 4+3j],
[2+5j, 5 ],
[ 3, 6+2j]])
>>> conj(u)
array([[ 0.-2.j, 4.-3.j],
[ 2.-5.j, 5.+0.j],
[ 3.+0.j, 6.-2.j]])
Transposé complexe conjugué#
>>> conj(u).T
array([[ 0.-2.j, 2.-5.j, 3.+0.j],
[ 4.-3.j, 5.+0.j, 6.-2.j]])
Tableaux et slicing#
Lors de la manipulation des tableaux, on a souvent besoin de récupérer une partie d’un tableau. Pour cela, Python permet d’extraire des tranches d’un tableau grâce une technique appelée slicing (tranchage, en français). Elle consiste à indiquer entre crochets des indices pour définir le début et la fin de la tranche et à les séparer par deux-points :.
>>> a = array([12, 25, 34, 56, 87])
>>> a[1:3]
array([25, 34])
Dans la tranche [n:m], l’élément d’indice n est inclus, mais pas celui d’indice m. Un moyen pour mémoriser ce mécanisme consiste à considérer que les limites de la tranche sont définies par les numéros des positions situées entre les éléments, comme dans le schéma ci-dessous :
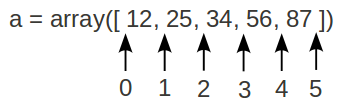
Il est aussi possible de ne pas mettre de début ou de fin.
>>> a[1:]
array([25, 34, 56, 87])
>>> a[:3]
array([12, 25, 34])
>>> a[:]
array([12, 25, 34, 56, 87])
Slicing des tableaux 2D#
>>> a = array([[1, 2, 3],
[4, 5, 6]])
>>> a[0,1]
2
>>> a[:,1:3]
array([[2, 3],
[5, 6]])
>>> a[:,1]
array([2, 5])
>>> a[0,:]
array([1, 2, 3])
Avertissement
a[:,n] donne un tableau 1D correspondant à la colonne d’indice n de a. Si on veut obtenir un tableau 2D correspondant à la colonne d’indice n, il faut faire du slicing en utilisant a[:,n:n+1].
>>> a[:,1:2]
array([[2],
[5]])
Tableaux de 0 - zeros()#
zeros(n) renvoie un tableau 1D de n zéros.
>>> zeros(3)
array([ 0., 0., 0.])
zeros((m,n)) renvoie tableau 2D de taille m x n, c’est-à-dire de shape (m,n).
>>> zeros((2,3))
array([[ 0., 0., 0.],
[ 0., 0., 0.]])
Tableaux de 1 - ones()#
>>> ones(3)
array([ 1., 1., 1.])
>>> ones((2,3))
array([[ 1., 1., 1.],
[ 1., 1., 1.]])
Matrice identité - eye()#
eye(n) renvoie tableau 2D carré de taille n x n, avec des uns sur la diagonale et des zéros partout ailleurs.
>>> eye(3)
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
Exercice
Effectuer le produit suivant :
Produire un tableau de taille 7 x 8 ne contenant que des 3.
Algèbre linéaire#
Déterminant - det()#
>>> a = array([[1, 2],
[3, 4]])
>>> det(a)
-2.0
Inverse - inv()#
>>> a = array([[1, 3, 3],
[1, 4, 3],
[1, 3, 4]])
>>> inv(a)
array([[ 7., -3., -3.],
[-1., 1., 0.],
[-1., 0., 1.]])
Résolution d’un système d’équations linéaires - solve()#
Pour résoudre le système d’équations linéaires 3 * x0 + x1 = 9 et x0 + 2 * x1 = 8 :
>>> a = array([[3,1], [1,2]])
>>> b = array([9,8])
>>> x = solve(a, b)
>>> x
array([ 2., 3.])
Pour vérifier que la solution est correcte :
>>> allclose(dot(a, x), b)
True
Valeurs propres et vecteurs propres - eig()#
>>> A = array([[ 1, 1, -2 ], [-1, 2, 1], [0, 1, -1]])
>>> A
array([[ 1, 1, -2],
[-1, 2, 1],
[ 0, 1, -1]])
>>> D, V = eig(A)
>>> D
array([ 2., 1., -1.])
>>> V
array([[ 3.01511345e-01, -8.01783726e-01, 7.07106781e-01],
[ 9.04534034e-01, -5.34522484e-01, -3.52543159e-16],
[ 3.01511345e-01, -2.67261242e-01, 7.07106781e-01]])
Les colonnes de V sont les vecteurs propres de A associés aux valeurs propres qui apparaissent dans D.
Exercice : Vérifier que les colonnes de V sont bien des vecteurs propres de A
Changement de la taille d’un tableau#
Il est possible de changer la taille d’un tableau en utilisant l’attribut shape de ce tableau.
>>> u = arange(1,16)
>>> u
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
>>> shape(u)
(15,)
>>> u.shape = (3,5)
>>> u
array([[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15]])
>>> shape(u)
(3, 5)
Obtention d’un tableau 2D ligne ou colonne#
>>> a = arange(1,6)
>>> a
array([1, 2, 3, 4, 5])
>>> a.shape = (1,size(a))
>>> a
array([[1, 2, 3, 4, 5]])
>>> a.shape = (size(a),1)
>>> a
array([[1],
[2],
[3],
[4],
[5]])
