Fonctions mathématiques avec NumPy#
Ces fonctions sont accessibles grâce à NumPy.
>>> import numpy
Fonctions trigonométriques#
numpy.sin(x) |
sinus |
numpy.cos(x) |
cosinus |
numpy.tan(x) |
tangente |
numpy.arcsin(x) |
arcsinus |
numpy.arccos(x) |
arccosinus |
numpy.arctan(x) |
arctangente |
Fonctions hyperboliques#
numpy.sinh(x) |
sinus hyperbolique |
numpy.cosh(x) |
cosinus hyperbolique |
numpy.tanh(x) |
tangente hyperbolique |
numpy.arcsinh(x) |
arcsinus hyperbolique |
numpy.arccosh(x) |
arccosinus hyperbolique |
numpy.arctanh(x) |
arctangente hyperbolique |
Fonctions diverses#
x**n |
x à la puissance n, exemple : x**2 |
numpy.sqrt(x) |
racine carrée |
numpy.exp(x) |
exponentielle |
numpy.log(x) |
logarithme népérien |
numpy.abs(x) |
valeur absolue |
numpy.sign(x) |
signe |
Fonctions utiles pour les nombres complexes#
numpy.real(x) |
partie réelle |
numpy.imag(x) |
partie imaginaire |
numpy.abs(x) |
module |
numpy.angle(x) |
argument en radians |
numpy.conj(x) |
complexe conjugué |
Exemple#
>>> import numpy as np
>>> x = np.array([ 2 + 3j, 1j, 1])
>>> np.real(x)
array([ 2., 0., 1.])
>>> np.imag(x)
array([ 3., 1., 0.])
>>> np.abs(x)
array([ 3.60555128, 1. , 1. ])
>>> np.angle(x)
array([ 0.98279372, 1.57079633, 0. ])
>>> np.conj(x)
array([ 2.-3.j, 0.-1.j, 1.-0.j])
Arrondis#
numpy.around(x,n) |
arrondi à n décimales |
numpy.trunc(x) |
retourne la partie entière du nombre (le nombre est tronqué) |
>>> x = np.array([3.73637, 5.4374345])
>>> np.around(x,2)
array([ 3.74, 5.44])
around(x,0) retourne l’entier le plus proche.
>>> np.around(x,0)
array([ 4., 5.])
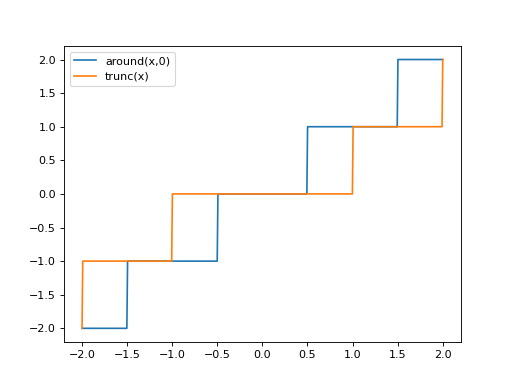
Comparaison entre around(x,0) et trunc(x)#
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 500)
plt.plot(x, np.around(x,0), label="around(x,0)")
plt.plot(x, np.trunc(x), label="trunc(x)")
plt.legend()
plt.show()
Nombres aléatoires#
La fonction numpy.random.random() permet d’obtenir des nombres compris entre 0 et 1 par tirage aléatoire avec une loi uniforme. Il faut noter que ces nombres aléatoires sont générés par un algorithme et ils ne sont donc pas vraiment « aléatoires » mais pseudo-aléatoires. Ceci peut poser problème quand on a besoin de produire un grand nombre de valeurs ou pour de la cryptographie car les tirages ne sont pas vraiment indépendants, il faut alors étudier plus en détail les algorithmes utilisés.
La fonction numpy.random.random() peut être utilisée avec des arguments pour obtenir des tableaux. Les arguments précisent alors la forme (shape) du tableau souhaité.
>>> np.random.random()
0.5540884899329033
>>> np.random.random(3)
array([ 0.86431861, 0.88519197, 0.30663316])
>>> np.random.random((2,3))
array([[ 0.66265691, 0.39385577, 0.09319192],
[ 0.43483474, 0.42859904, 0.79189574]])
