Visualisation d’une fonction à valeurs complexes avec PyLab

On cherche à visualiser une fonction \(z = f(x)\) où \(x\) est un réel et \(z\) un nombre complexe.

On va prendre comme exemple la fonction \(f(x)=5e^{i2x}+7e^{i3x}\).

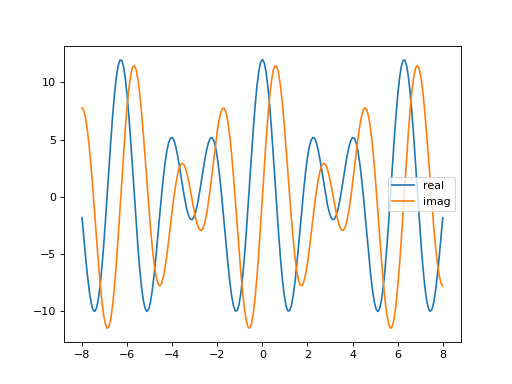
Visualisation de la partie réelle et de la partie imaginaire

from pylab import *

x = linspace(-8,8,201)
z = 5*exp(2j*x) + 7*exp(3j*x)

plot(x,real(z),label='real')
plot(x,imag(z),label='imag')
legend()

show()

(Source code)

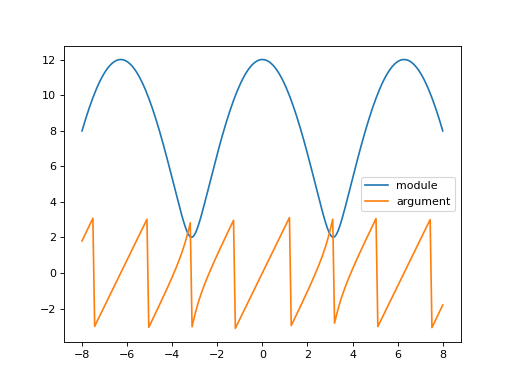
Visualisation du module et de l’argument

from pylab import *

x = linspace(-8,8,201)
z = 5*exp(2j*x) + 7*exp(3j*x)

plot(x,abs(z),label='module')
plot(x,angle(z),label='argument')
legend()

show()

(Source code)

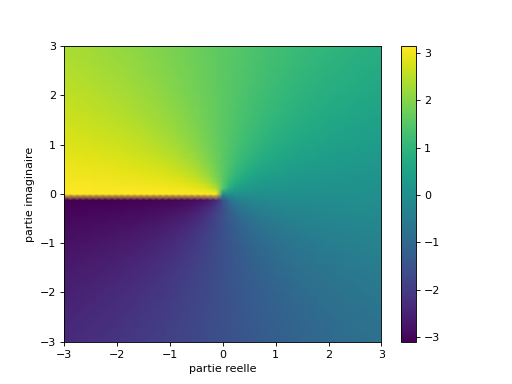
Visualisation de l’argument grâce à des couleurs

Une idée peut être d’associer une couleur à l’argument d’un nombre complexe. Pour cela, nous allons essayer de visualiser les arguments pour le plan complexe.

from pylab import *

x = linspace(-3, 3, 51)
y = linspace(-3, 3, 51)
X, Y = meshgrid(x, y)

C = angle(X + 1j *Y) 

pcolormesh(X, Y, C, shading='gouraud')
colorbar()
xlabel('partie reelle')
ylabel('partie imaginaire')

show()

(Source code)

Pour éviter la discontinuité quand l’argument vaut \(-\pi\), nous allons choisir l’échelle de couleur hsv.

from pylab import *

x = linspace(-3, 3, 51)
y = linspace(-3, 3, 51)
X, Y = meshgrid(x, y)

C = angle(X + 1j *Y) 

pcolormesh(X, Y, C, shading='gouraud', cmap=cm.hsv)
colorbar()
xlabel('partie reelle')
ylabel('partie imaginaire')


show()

(Source code)

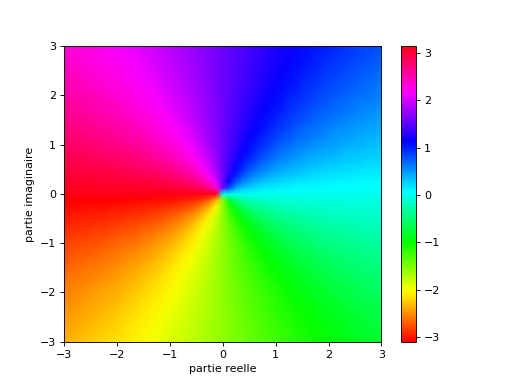
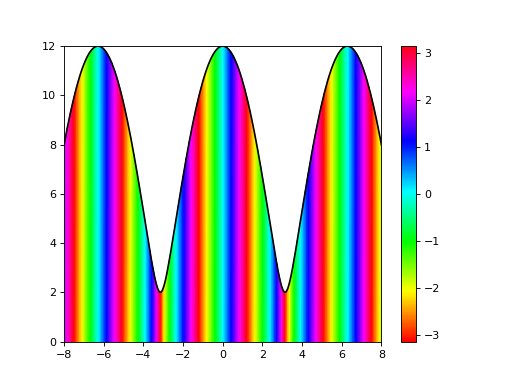
Nous pouvons alors au final construire la visualisation suivante :

from pylab import *

x = linspace(-8,8,201)
z = 5*exp(2j*x) + 7*exp(3j*x)

X = array([x,x])

y0 = zeros(len(x))
y = abs(z)
Y = array([y0,y])

Z = array([z,z])
C = angle(Z)

plot(x,y,'k')

pcolormesh(X, Y, C, shading='gouraud', cmap=cm.hsv, vmin=-pi, vmax=pi)
colorbar()

show()

(Source code)