Visualisation d’une fonction à valeurs complexes avec Python

Pour tracer une fonction à valeurs complexes, par exemple la fonction d’ondes en Mécanique Quantique, il est possible d’envisager plusieurs stratégies. Dans cette page, nous verrons une stratégie basée sur l’utilisation d’une échelle colorée pour les nombres complexes.

Exemple

Nous allons considérer une fonction \(z = f(x)\) où \(x\) est un réel et \(z\) un nombre complexe.

On va prendre comme exemple la fonction \(f(x)=5e^{i2x}+7e^{i3x}\).

Voici un exemple de figure que l’on pourra obtenir :

(Source code)

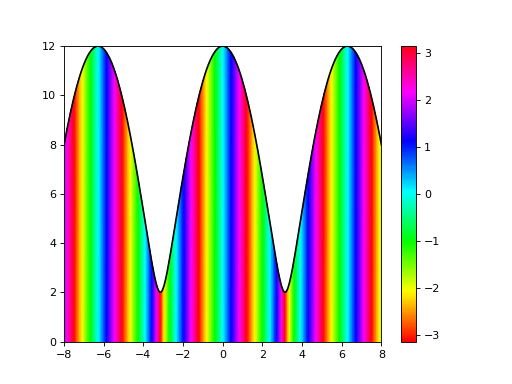
Visualisation de la partie réelle et de la partie imaginaire

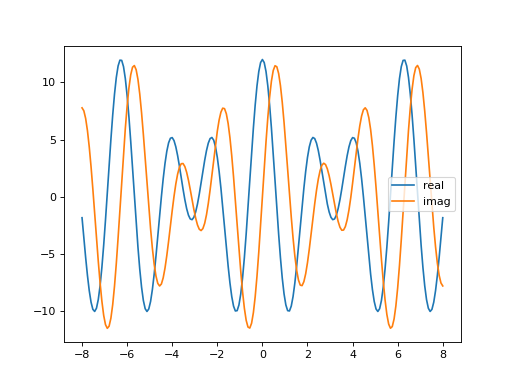
Une première approche peut consister à tracer partie réelle et partie imaginaire.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-8, 8, 201)
z = 5*np.exp(2j*x) + 7*np.exp(3j*x)

plt.plot(x, np.real(z), label="real")
plt.plot(x, np.imag(z), label="imag")
plt.legend()

plt.show()

(Source code)

Visualisation du module et de l’argument

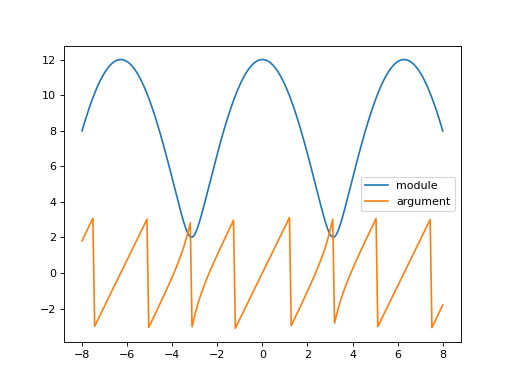
Une deuxième approche peut représenter le module et l’argument.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-8, 8, 201)
z = 5*np.exp(2j*x) + 7*np.exp(3j*x)

plt.plot(x, np.abs(z), label="module")
plt.plot(x, np.angle(z), label="argument")
plt.legend()

plt.show()

(Source code)

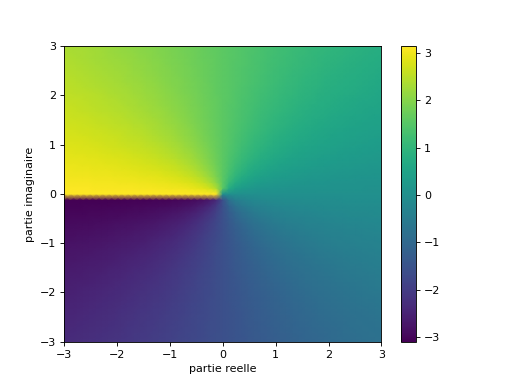
Visualisation de l’argument grâce à des couleurs

Une idée peut être d’associer une couleur à l’argument d’un nombre complexe. Pour cela, nous allons essayer de visualiser les arguments pour le plan complexe.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3, 3, 51)
y = np.linspace(-3, 3, 51)
X, Y = np.meshgrid(x, y)

C = np.angle(X + 1j *Y) 

plt.pcolormesh(X, Y, C, shading="gouraud")
plt.colorbar()
plt.xlabel("partie reelle")
plt.ylabel("partie imaginaire")

plt.show()

(Source code)

Pour éviter la discontinuité quand l’argument vaut \(-\pi\), nous allons choisir l’échelle de couleur hsv.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3, 3, 51)
y = np.linspace(-3, 3, 51)
X, Y = np.meshgrid(x, y)

C = np.angle(X + 1j *Y) 

plt.pcolormesh(X, Y, C, shading="gouraud",  cmap=plt.cm.hsv)
plt.colorbar()
plt.xlabel("partie reelle")
plt.ylabel("partie imaginaire")

plt.show()

(Source code)

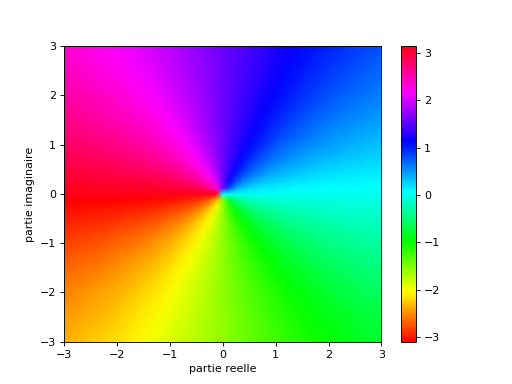
Nous pouvons alors au final construire la visualisation suivante :

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-8, 8, 201)
z = 5*np.exp(2j*x) + 7*np.exp(3j*x)

X = np.array([x,x])

y0 = np.zeros(len(x))
y = np.abs(z)
Y = np.array([y0,y])

Z = np.array([z,z])
C = np.angle(Z)

plt.plot(x, y, "k")

plt.pcolormesh(X, Y, C, shading="gouraud", cmap=plt.cm.hsv, vmin=-np.pi, vmax=np.pi)
plt.colorbar()

plt.show()

(Source code)